The Power of Being Equal
“Masters, give unto your servants that which is just and equal; knowing that ye also have a Master in heaven.” Colossians 4:1 KJV
As long as I can remember I’ve been interested in mathematics. I’m not real sure when it started, but my guess is that it came from watching my Dad. When I was a young kid, I sometimes was lucky enough to go to work with my Dad. My father sold bread to grocery stores.
There were many varieties of bread my Dad sold, but all the same types of bread came in its own box. After he went into the store to see what types and quantity of bread they needed, he would return to his truck and start pulling different types of bread, from different boxes, and put it into another box that he would take into the store.
Next, my Dad would write the quantity of each type of loaf he put in his store box in a spot on a long order pad. There was a piece of carbon paper he stuck between two sheets so there would be one copy for the store and another copy for him to turn into his office the next morning so his company could get paid for the bread delivered to the store.
Before my father would take the bread into the store, he would tally the little sheet so he could arrive at a total cost of what he was delivering. He would take the quantity of each type of loaf and multiply it by the cost for each loaf to get a subtotal for that item. After he did this for each item, he would add them all together to get a grand total.
Today, with hand held computers, that might not seem to be such a hard thing to do, but you must realize this was in the days before calculators and computers were available to the common man. My Dad had to do all this in his head and he was pretty quick at doing it. I would look on in awe at how fast he could do it. Maybe that’s what sparked a mathematical interest in me.
When I was in high school, calculators were just starting to come on the market. This “new, modern” technology was pretty expensive. Most families, like mine, couldn’t afford to have a luxury item like that. In fact, we were not even allowed to use a calculator in high school.
The highest level of mathematics in my high school, at the time, was Algebra 2. For things like sine, cosines, tangents, and square roots we had to look at charts in the back of the books for numbers to use in our calculations. We didn’t push buttons, we wrote out equations on paper and worked out the answers in our heads.
The county my high school was in had a special program for students who maintained at least a “B” average. We were allowed to take a free course at the community college for our efforts. Since our high school only offered mathematics up to Algebra 2, I decided to take one of those free courses. I took Trigonometry.
On the first night of my Trigonometry class, it was revealed that we would be allowed to use calculators in the class. In fact, it was recommended that we get one to use. My parents splurged and got me one that did more than just add, subtract, multiply and divide. I treasured that calculator like it was a piece of gold.
To me, one of the most fascinating things about mathematics is the equal sign. Basically, an equal sign means that whatever is to the left of the equal sign has to have the same value as what is on the right of the equal sign.
For example, let’s say you have a five pound rock on one side of the equal sign. To balance it you must have five pounds worth of rocks on the other side of the equal sign. So, you could have one five pound rock on one side and one five pound rock on the other side (5=5). But you could have two different weight rocks on the other side, like one three pound rock and one two pound rock (3+2) or one four pound rock and one one pound rock (4+1), and it would still equal the weight of the five pound rock.
It doesn’t stop there though. Let’s say you have five one pound rocks (5×1), you would also equal the weight of the five pound rock on the other side. If you had a ten pound rock, you could break it in half (10/2) and you would also have a five pound rock equal to the five pound rock on the other side.
The Bible is full of math. There are numbers everywhere. God used a very basic formula to get our mathematics off to a roaring start. God said: “day one (first day) + day two (second day) + day three (third day) + day four (fourth day) + day five (fifth day) + day six (sixth day) = a day of rest (seventh day).”
God then tells Adam and Eve to multiply. When Adam and Eve sat down at a table and pulled out a piece of paper, God must have been confused. When they started writing numbers on the paper with an “x” between them, He probably corrected them by saying that was not what He meant by multiply.
A few pages later, in the Bible, Noah gets into the act. If Noah didn’t know what a 2×4 was, this ark building thing was going to take a very long time to build. To understand the ruler that he used to measure the boards, Noah had to know that the little marks on that ruler represented eighths, quarters, and half inches. Then there were a lot of animals to count which amounted to even more numbers to keep up with.
God even gave one Book of the Bible a mathematical name: Numbers. There was a lot of counting and adding going on in those chapters of that Book. Let’s not forget some of the other first Old Testament Books that describe the Temple and articles that were supposed to go in it. God didn’t want one cherub resting on the Ark of the Covenant without another one sitting on the other side to balance it out. He also told them the exact dimensions He wanted everything to be.
There were seven days in a week, two of each animal in the ark, forty (and the number forty is used over 140 times in the Bible) days and nights of rain. Twelve is the number of the tribes of Jacob, which matches the number of disciples Jesus picked. From a heavenly perspective there are three parts of the Trinity, but there is only one God. Let’s not forget that after six days of marching once around Jericho’s wall, and seven times on the seventh day, the Israelites watched it fall. The Ten Commandments were given to Moses, which were so important that God personally wrote them on stone for him so he wouldn’t forget them. We won’t even talk about that scary 666 number.
Many, many years ago, people sat around and figured out all these mathematical things for us. All I have to do is enjoy the fruits of their labor. To start the process of thinking these things out they gave the process a fancy name called theorem. Once that theorem passes the test where many, many smart people can’t prove it wrong because many, many other smart people are proving it true, it gets another name. It can be called a law or a property.
One of my favorite “properties” is the Transitive Property. What the Transitive Property states is that if A=B and B=C, then A=C. Sounds simple enough, but it is really amazing. So amazing, in fact, that I think it can be applied to life itself.
Let’s say you want to buy a car. You have $300 in your budget each month that you can afford to spend on a new car. Now, let’s say you find the perfect car where the payments are $300 a month and you get the car. You are so happy.
Using our equation, $300 = a car. A car = a happy person. So, $300 = happy (or $300 made you happy).
While I was at the community college, taking my trigonometry class, I learned another theorem. This is a theorem that applies to right angled triangles. It was a theorem called the Pythagorean Theorem. It states that A2 + B2 = C2. A and B are the short sides of the right triangle and C is the longest side of that right triangle, or the hypotenuse.
A Greek philosopher, named Pythagoras, got his name attached to this theorem around the sixth century BC. Despite the fact that he appears to be the hero of this mathematical marvel, it was well-known many years before he was even born. A full thousand years before Pythagoras was around, the Babylonians knew of it. I guess the term Babylonian Formula or Theorem sounded too much like some evil drink you would give a baby which was acting up or a poison you might be forced to drink in the damp cellar of one of those medieval castles by a wicked wizard.
Most people, who know far more about this than I do, are almost certain the Egyptians knew of this theorem when they were building the pyramids around 2550 BC. China, India, and most of Mesopotamia also knew of it by 600 BC. In fact, the only logical reason we Americans didn’t know about it was that we weren’t even a country yet.
Since this theorem has been around a very long time, I’m not exactly sure why it has never become a law. Many, many people have proven it true, and as far as I know, no one has proven it wrong.
One of the amazing facts about proving the Pythagorean Theorem is that one of our Presidents actually wrote a piece in the New-England Journal of Education with his proof that the theorem was true. His proof went like this:
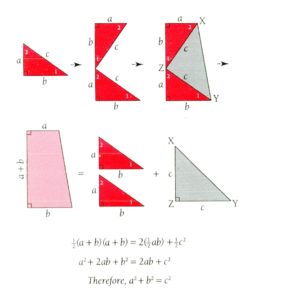
For those of you who don’t think any of our Presidents have been any too smart, especially academically, this one would probably be the greatest example to dispute that thought. Sure, you have Thomas Jefferson who seemed to know a little bit about everything and whose Monticello tours highlight his brilliance. Jefferson was an incredible learner, and even more impressive at applying what he learned. But this far lesser known President was just plain smart.
Learning Latin, or even Greek for that matter, would be a very difficult task. I have a hard enough time with English, as many of you, who have read my blogs, may be well aware of. This President not only knew Latin and Greek, but he could write one of them with his left hand while he was writing the other with the right hand.
The New-England Journal of Education’s volume III, number 14, dated April 1, 1876 debuted James Garfield’s proof that the Pythagorean Theorem was true. Yes, while America was getting ready to celebrate its 100th birthday, the brilliant James Garfield was spending his time proving a mathematical phenomenon that was thousands of years old. I thought I had a love of mathematics, but my love for it was never even close to how much Garfield loved it.
Before James Garfield decided he wanted to enter politics, he wanted to be a mathematics professor. When he was in the House of Representatives, Garfield loved to talk mathematics. I’m sure this made him the joy of the chamber. Many a laugh was probably shared over his talk of analytic equations. Actually, there was probably more than one member scouting for the exits when he came within eyesight.
God doesn’t love sin. In fact, He hates it so much that He doesn’t even want to be in the same room with it. So here we go: Our life = sinful choices. Sinful choices = no God. So our lives = no God because of those sinful choices. Sounds like we are doomed.
But God has another principle (or law) that even overrides the one above. This very basic principle is outlined in the Bible. It basically states: God and His presence = love. His love = sending His Son to save us. Sending Jesus (His Son) to save us = God being able to have us in His presence. For all the math in the Bible, that is God’s favorite equation.
Prayer: Dear Mighty Father, Sometimes the math in my life doesn’t work because of my sinful nature. Please help me always seek Jesus to balance the equation. Amen.
For more information on James Garfield’s proof of Pythagorean Theorem please visit: https://www.maa.org/press/periodicals/convergence/mathematical-treasure-james-a-garfields-proof-of-the-pythagorean-theorem (proof diagram above is from this website)



